Motion computation via an unsupervised-learning approach (pt.3)
- 23 minsThis blog-post is a direct continuation of the previous one.
Fourier-domain optimization (continued)
Recall that we are formulating our optimization objective in the Fourier-domain, the motivations for which will hopefully be made clearer in the close future. So far we’ve seen that a Fourier-domain implementation is possibly faster than a spatial-domain one, depending on our exact objective formulation, inputs, etc… In this current blog-post we will also obtain some necessary intuition about the nature of our optimization task, through its Fourier-domain interpretation.
Just to remind, our Fourier-domain objective formulation is:
where
We’ve seen that the rational component is known in its transfer-function form as a moving-average filter. We will learn more about the nature of this filter in this current blog-post, as well as why it is insufficient in itself for successful Fourier-domain optimization.
First optimization trial (naive)
In order to compute the motion of an input video, we need to slightly tweak our Fourier-objective (recall that it is a function of the displacement $\Delta\phi$, which we do not know at the time of computation, as it depends on the ground-truth shift $\theta*$) We must take this into account then in our code-implementation, more specifically, instead of computing the analytical closed-form geometric sum, we need to explicitly compute the sum from the input frames. We obtain then the following implementation
def fourier_pipeline_video(frames: torch.Tensor, shifts: torch.Tensor,
fourier_input=False):
"""
Fully differentiable Fourier-domain warping and integration.
Args:
frames: (B, T, H, W) spatial frames
shifts: (B, 2) shift vector per batch
Returns:
integrated_fft: (B, H, W) integrated FFT
total_power: (B,) variance-like scalar
"""
B, T, H, W = frames.shape
if not fourier_input:
# frames_windowed = apply_spatial_window(frames)
X = torch.fft.fft2(frames, norm='forward', dim=(-2, -1))
else:
X = frames
# Frequency grids
v, u = torch.meshgrid(
torch.arange(H, device=frames.device, dtype=X.real.dtype),
torch.arange(W, device=frames.device, dtype=X.real.dtype),
indexing='ij'
)
shifts_exp = shifts.view(B, 1, 1, 2) # (B,1,1,2)
# Correct Fourier normalization: dx along width (u), dy along height (v)
omega = (u.unsqueeze(0) * shifts_exp[..., 0] / W + v.unsqueeze(0) * shifts_exp[..., 1] / H) # (B,H,W)
omega = omega.unsqueeze(1) # (B,1,H,W)
base_phase = torch.exp(-2j * torch.pi * omega)
t = torch.arange(T, device=frames.device, dtype=X.real.dtype).view(1, T, 1, 1)
phase_shifts = (base_phase * (1 - base_alpha)) ** t if weighted else base_phase ** t # (B,T,H,W)
# Apply phase shifts
shifted = X * phase_shifts # (B,T,H,W)
# Integrate along T
integrated_fft = shifted.sum(dim=1) / T
# Compute variance
mag2 = integrated_fft.real ** 2 + integrated_fft.imag ** 2
dc_power = mag2[..., 0, 0]
variance_fft = mag2.sum(dim=(-2, -1)) - dc_power
return integrated_fft, variance_fft
Note that the spatial pipeline can already deal with video input (see first blogpost in the series). We now provide some code for running the optimization procedure in both domains and comparing the results (feel free to skip this)
import itertools
# estimated shifts should be within this distance from GT for successful optimization
SUCCESS_CRIT = 1/T
# Wrappers for evaluating functions
fourier_wrapper = lambda videos, shifts, weighted: fourier_pipeline_video(videos, shifts, weighted=weighted, fourier_input=True, interpolate=True)
spatial_wrapper = lambda videos, shifts, weighted: spatial_pipeline(videos, videos.shape[1], shifts, weighted=weighted)
def compute_motion(eval_fn, videos, max_steps=400, thresh=SUCCESS_CRIT, num_trials=T, verbose=False):
"""
Compute motion via optimization over videos using eval_fn (spatial/fourier pipeline).
Keep track of convergence statistics for later.
"""
def initialize_shifts(n_trial):
# For reproducibility
torch.manual_seed(n_trial)
# Helper: generate initial shifts for optimization randomly
init_shifts = (torch.rand(2*B).reshape(B,2) * 2 - 1) * (B*SHIFT_SCALE)
return init_shifts.clone().detach().requires_grad_(True)
all_trials_results = []
for trial in range(num_trials):
shifts = initialize_shifts(trial)
# Optimizer and scheduler
optimizer = torch.optim.Adam([shifts], lr=0.5)
scheduler = torch.optim.lr_scheduler.ReduceLROnPlateau(optimizer, mode='min', patience=50, factor=0.5)
all_shifts = []
deviations = []
converged = False
for step in range(max_steps):
optimizer.zero_grad()
# Forward pass
_, _, var_batches = fourier_wrapper(videos, shifts) if eval_fn == "fourier" \
else spatial_wrapper(videos, shifts)
# Stochastic loss
loss = -var_batches.mean()
loss.backward()
optimizer.step()
scheduler.step(loss)
# Track deviation
current_shifts = shifts.detach().clone()
deviation = torch.norm(current_shifts - GT_SHIFTS).item()
all_shifts.append(current_shifts)
deviations.append(deviation)
if deviation < thresh and step > 100:
converged = True
# print(f"Converged at step {step}")
break
trial_result = {
'final_shifts': all_shifts[-1],
'final_deviation': deviations[-1],
'converged': converged,
'steps': step + 1,
'all_shifts': all_shifts,
'deviations': deviations
}
all_trials_results.append(trial_result)
# Count number of successful convergences
num_converged = sum(1 for r in all_trials_results if r['converged'])
if verbose: print(f"Total successful convergences: {num_converged}/{num_trials}")
return all_trials_results, num_converged
def compare_configs(configurations, inputs, num_trials=10, verbose=True, **kwargs):
"""
Experiment setup: given input configurations of form (eval_fn="fourier/spatial", weighted="True/False"), evaluate how well
motion computation works for each such configuration
"""
comparison_results = {}
success_counts = {}
input_spatial, input_fourier = inputs
if verbose:
# Give some initial information
print(f"GT shifts: {GT_SHIFTS}")
for config in configurations:
eval_fn = config
videos = input_spatial.clone().detach().requires_grad_(True) if eval_fn=="spatial" else \
input_fourier.clone().detach().requires_grad_(True)
config_name = f"{eval_fn}"
if verbose: print(f"\n=== Running {config_name} pipeline ===")
results, num_converged = compute_motion(
eval_fn=eval_fn,
videos=videos,
num_trials=num_trials,
verbose=verbose,
**kwargs # Pass all additional arguments
)
comparison_results[config_name] = results
success_counts[config_name] = num_converged
# Print summary of convergences
if verbose:
print("\n=== Convergence Summary ===")
for config_name, num_converged in success_counts.items():
print(f"{config_name}: {num_converged}/{num_trials} successful convergences")
return comparison_results, success_counts
#give both inputs for relevant configurations
methods = ["spatial", "fourier"]
# try Fourier methods in easy mode with higher threshold
results, _ = compare_configs(methods, (input_spatial, input_fourier))
We run this code, obtaining the following
GT shifts: tensor([[ 4, 2],
[ 0, -2]])
=== Running spatial pipeline ===
Total successful convergences: 10/10
=== Running fourier pipeline ===
Total successful convergences: 0/10
Huh, what went wrong? Let’s plot the loss landscapes to get a better idea
# Plot loss contour and optimization path
N = 20 # number of initial steps to plot
batch_idx = 0 # batch to visualize
shift_range = 2*B*SHIFT_SCALE
mesh_resolution = shift_range**2 # number of points per axis
# Grid for contour
x = torch.linspace(-shift_range, shift_range, mesh_resolution)
y = torch.linspace(-shift_range, shift_range, mesh_resolution)
X_grid, Y_grid = torch.meshgrid(x, y, indexing='ij')
# Prepare figure
fig, axes = plt.subplots(len(configurations)//2, 2, figsize=(14, 12))
axes = axes.flatten()
for idx, (method, weighted) in enumerate(configurations):
# Compute loss grid
loss_grid = torch.zeros_like(X_grid)
if method == "spatial":
frames_plot = input_spatial.clone().detach().requires_grad_(False)
pipeline_fn = spatial_pipeline
else: # Fourier
frames_plot = input_fourier.clone().detach().requires_grad_(False)
pipeline_fn = lambda f, T, s: fourier_pipeline_video(f, s, fourier_input=True)
for i in range(mesh_resolution):
for j in range(mesh_resolution):
test_shift = torch.zeros(B, 2)
test_shift[batch_idx, 0] = X_grid[i,j]
test_shift[batch_idx, 1] = Y_grid[i,j]
_, _, var_batch = pipeline_fn(frames_plot, frames_plot.shape[1] if method=="spatial" else T, test_shift)
loss_grid[i,j] = var_batch[batch_idx].item()
# Convert to numpy for plotting
X_np, Y_np, Z_np = X_grid.numpy(), Y_grid.numpy(), loss_grid.numpy()
# Contour plot
ax = axes[idx]
contour = ax.contourf(X_np, Y_np, Z_np, levels=50, cmap='viridis')
fig.colorbar(contour, ax=ax)
ax.set_title(f"{method.capitalize()}")
ax.set_xlabel('Shift dx')
ax.set_ylabel('Shift dy')
# Overlay first N steps of optimization
trial_result = results[f"{method}"][0] # pick first trial
shifts_for_plot = trial_result['all_shifts'][:N]
shifts_np = torch.stack(shifts_for_plot).numpy()[:, batch_idx, :]
ax.plot(shifts_np[:,0], shifts_np[:,1], 'r-o', label='Optimization steps')
ax.scatter(GT_SHIFTS[batch_idx,0], GT_SHIFTS[batch_idx,1], color='red', marker='x', s=60, label='GT')
ax.legend()
plt.tight_layout()
plt.show()
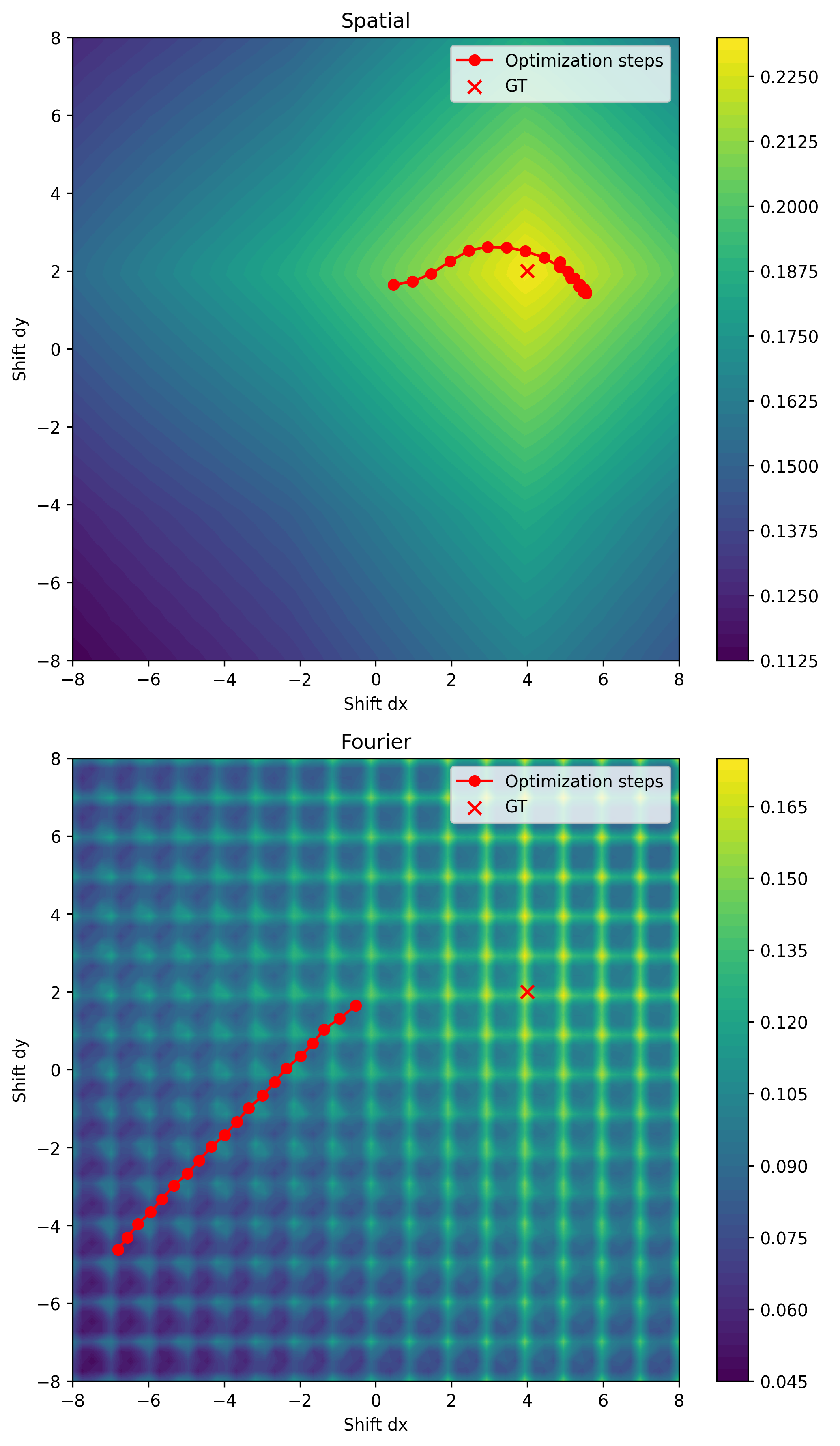
Hmm, the loss landscapes do not look the same at all. While the spatial domain implementation results in a smooth landscape, in the Fourier-domain we get a certain “grid”-ness which is a bit hard to make sense of. More specifically we have periodic local maxima (at integer-valued shifts), which disrupt optimization. In order to better understand this phenomenon let’s analyse the behavior of the previously-mentioned moving-average filter, and see what it has to do with it.
Moving average filter- frequency response
We begin by finding an analytical representation for the moving average filter frequency response, via
Note that we have separated the moving-average filter into phase and magnitude components, meaning that computing the frequency response from here is straightforward. The magnitude usually ends up looking something like (found this online, forgive the spelling mistake in the title) 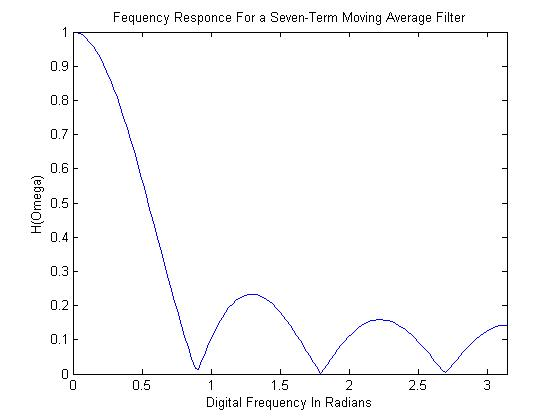
Where in this case we see the magnitude spectrum of a 7-tap ($T=7$) moving-average filter. We see that the filter generally has a low-pass behavior, with certain ‘richochets’ or rebounds of magnitude, which we will see later lead to all kinds of problems.
Let’s get some perspective on the filter from an experienced practitioner, via The Scientist and Engineer’s Guide to Digital Signal Processing:
Not only is the moving average filter very good for many applications, it is optimal for a common problem, reducing random white noise while keeping the sharpest step response. Of all the possible linear filters that could be used, the moving average produces the lowest noise for a given edge sharpness. The amount of noise reduction is equal to the square-root of the number of points in the average.
On the one hand then, this is the “filter for the job”, in the sense that once we begin to deal with occlusion, we will want to choose a filter which gets rid of noise (occlusion) optimally for our optimization purposes.
One the other hand, just a few pages later we get the following
The roll-off is very slow and the stopband attenuation is ghastly. Clearly, the moving average filter cannot separate one band of frequencies from another. In short, the moving average is an exceptionally good smoothing filter (the action in the time domain), but an exceptionally bad low-pass filter (the action in the frequency domain).
Now then, looking back to the loss landscape for the Fourier optimization objective, we perceive a general trend of increase in variance (signal energy) when approaching the ground truth shift, but an additional side-effect is a radial-oscillation pattern prevalent around integer-valued shifts, where energy seems to spike. This phenomenon is a type of spectral-leakage.
Given our newly-gained knowledge about the behavior of the moving-average filter and its less-than-sufficient attenuation, we can interpret this oscillation as an artifact caused by the “left-over” high-frequency components after filtering. In other words, we need additional attenuation of high-frequency content in the integrated image for optimization to work, meaning that additional low-pass filtering is necessary.
Bilinear interpolation as a low-pass filter
Going back to the difference between spatial and Fourier domains, we note that the one operation which we didn’t previously address was bilinear interpolation in the frame warping. The initial motivation for this operation was to ensure differentiability for the spatial-domain optimization (recall that “rolling” the image frames is non-differentiable), where “bilinear interpolation is arguably the simplest possible separable method that produces a con- tinuous (differentiable) function”1. Consequently, the operation has profound consequences in the Fourier domain as well.
Let’s get to know these by modelling the operator first as a kernel in the time/spatial domain, and then looking at its Fourier-equivalent operator.
The linear interpolation kernel (also called the triangular kernel) is defined as
For bilinear interpolation in two dimensions, we use the separable extension of this kernel. If $k(t)$ is the 1-D interpolation kernel, then the 2-D bilinear interpolation kernel is
This means that bilinear interpolation is performed by convolving the signal/image first along one axis using k, and then along the other axis using the same kernel.
The triangular kernel can be written as the convolution of two rectangular functions:
This proves useful for computing the Fourier transform of the kernel, where using the dualities $\circledast \;\overset{\text{FT}}{\longleftrightarrow}\; \times , \operatorname{rect} \overset{\text{FT}}{\longleftrightarrow} \operatorname{sinc}$ (see this blogpost) we get:
Meaning the bilinear interpolation kernel is equivalent to a squared sinc function in the frequency domain. What is the interpretation of the frequency response of this filter? Obviously it is quite close in nature to the squared frequency response of the moving average filter, but whereas the latter is periodic, sinc decays over time. We can easily show that the former has better high-frequency suppression, via the inequality
Where the last two expressions are the moving average filter and bilinear interpolation frequency responses respectively. It makes sense then to apply both of these operations to obtain a smoother, more convex optimization landscape. We can exhibit this behavior by looking at the frequency responses of each of the filters, as well as a cascade (product in the frequency-domain) of the two: 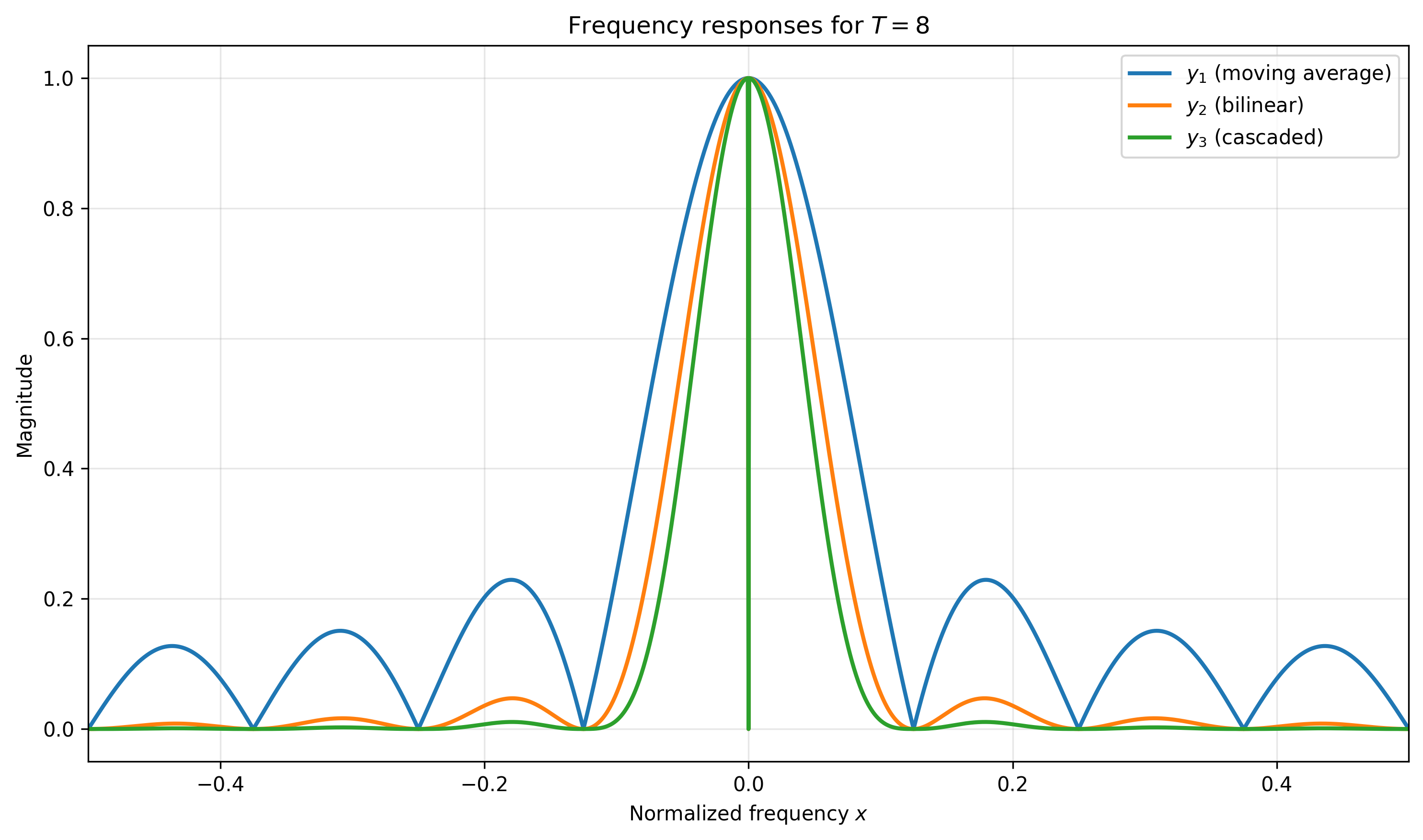
Note that the cascaded filters frequency response (green) has virtually no magnitude for frequency beyond the stop-band frequency of $\frac{1}{T}=0.125$, meaning our optimization landscape should now be in much better shape!
Second optimization trial (with interpolation)
We implement the frequency-domain interpolation in code as follows:
def make_sinc_2d(u, v, W, H):
# Separate u and v components for proper 2D bilinear
u_norm = u.unsqueeze(0) / W # Normalized frequencies
v_norm = v.unsqueeze(0) / H
# 2D separable bilinear kernel
sinc_u = torch.sinc(u_norm) ** 2 # Smooth in u-direction
sinc_v = torch.sinc(v_norm) ** 2 # Smooth in v-direction
sinc_2d = sinc_u * sinc_v
return sinc_2d
And incorporate it into our own existing code
def fourier_pipeline_video(frames: torch.Tensor, shifts: torch.Tensor,
weighted=False, fourier_input=False, base_alpha=BASE_ALPHA,
interpolate=False
):
"""
Fully differentiable Fourier-domain warping and integration.
Args:
frames: (B, T, H, W) spatial frames
shifts: (B, 2) shift vector per batch
weighted: whether to apply geometric weighting
Returns:
shifted: (B, T, H, W) phase-shifted FFTs
integrated_fft: (B, H, W) integrated FFT
total_power: (B,) variance-like scalar
"""
# no change to previous code
...
if interpolate:
# implement bilinear interpolation
sinc_2d = make_sinc_2d(u, v, W, H)
shifted = X * phase_shifts * sinc_2d.unsqueeze(1) # Apply to all frames
else:
shifted = X * phase_shifts # (B,T,H,W)
# no change to next code
...
return shifted, integrated_fft, total_power
We are now ready to run our code once more, obtaining the following optimization results
GT shifts: tensor([[ 4, 2],
[ 0, -2]])
=== Running spatial pipeline ===
Total successful convergences: 10/10
=== Running fourier pipeline ===
Total successful convergences: 10/10
and the following loss landscape 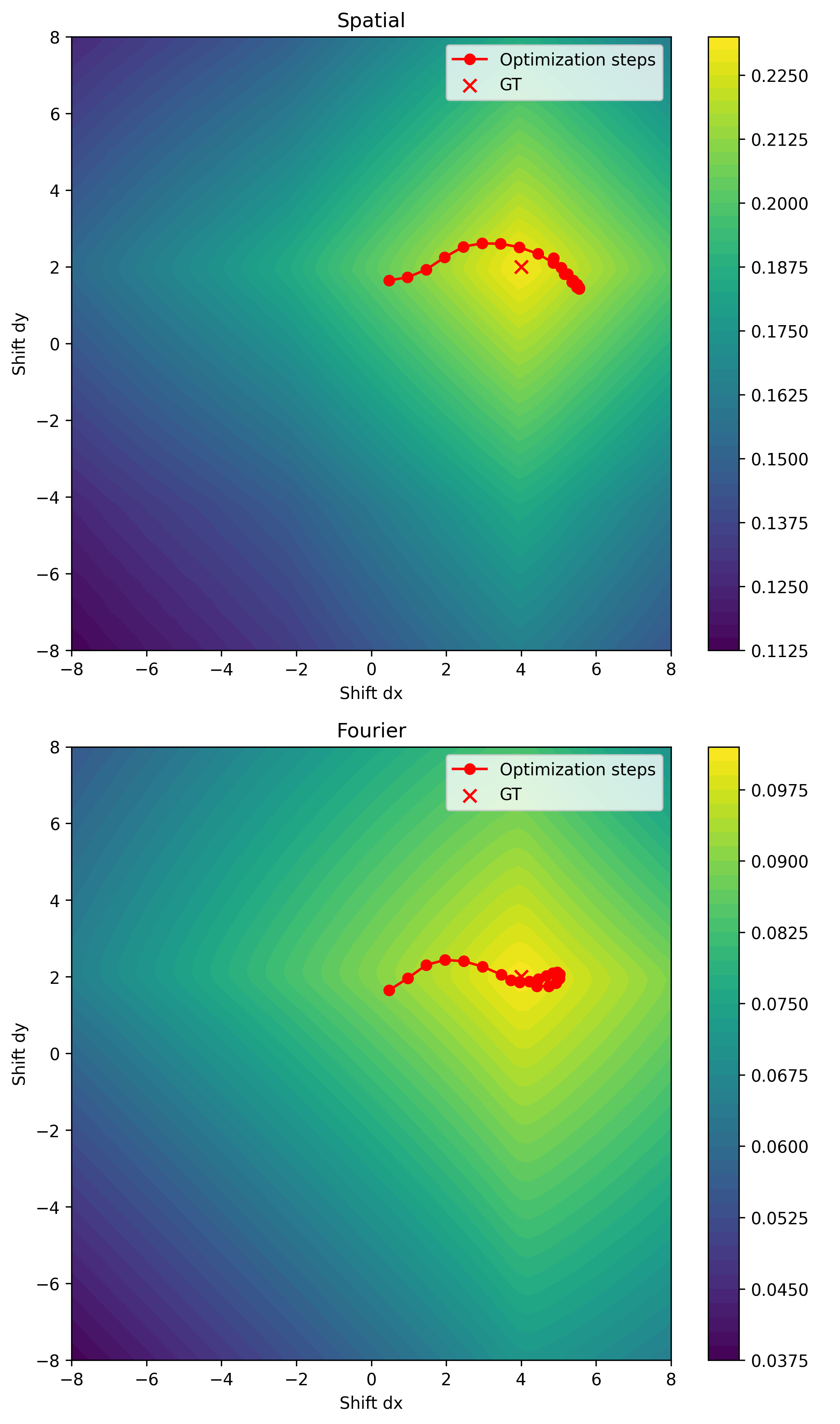
Success! Note also that the shift estimates in the Fourier domain appear to converge slightly faster (end up generally closer) to the ground truth shift than in the spatial-domain case.
Conclusion
We’ve discovered that not only is bilinear interpolation sufficient for optimization (by providing differentiability in the spatial domain implementation), but it is also necessary for ensuring that our optimization landscape is smooth and convex.
Note however that in our Fourier domain implementation we are not bound to use interpolation (as in the spatial domain case, where it is very efficient to compute), but rather may choose any suitable low-pass filters. There are better possibilities out there, such as the Lanczos filter, which may pop back in the next blog-posts! Stay tuned.
Next time, we’ll take a look at some of the more theoretical aspects of the problem, mostly through the connection of our optimization objective to a well-known signal processing algorithm known as generalized cross-correlation phase transform (GCC-PHAT). We will go down to 1D for more simplified analytical forms, which will once more give us additional intuition. Most importantly, we will begin discussing possible models for occlusion, and see how these affect our notion of the problem, objective, etc…
See you next time!
-
P. Getreuer, “Linear Methods for Image Interpolation.” Image Processing On Line, 2011. DOI: 10.5201/ipol.2011.g_lmii. ↩